정렬 ) O(N^2)의 대표적인 정렬 방법

이번 포스트에서는 정렬 알고리즘의 가장 기본이 되는 세 가지의 알고리즘을 알아보고 같은 문제를 각각의 알고리즘을 적용하여 풀이해보겠습니다. O(n^2)의 시간복잡도를 가지는 효율이 낮은 정렬 방법들이지만, 코딩테스트 문제의 시간 조건이 충분할 때 간단하게 구현할 수 있습니다.

▪︎ 선택 정렬

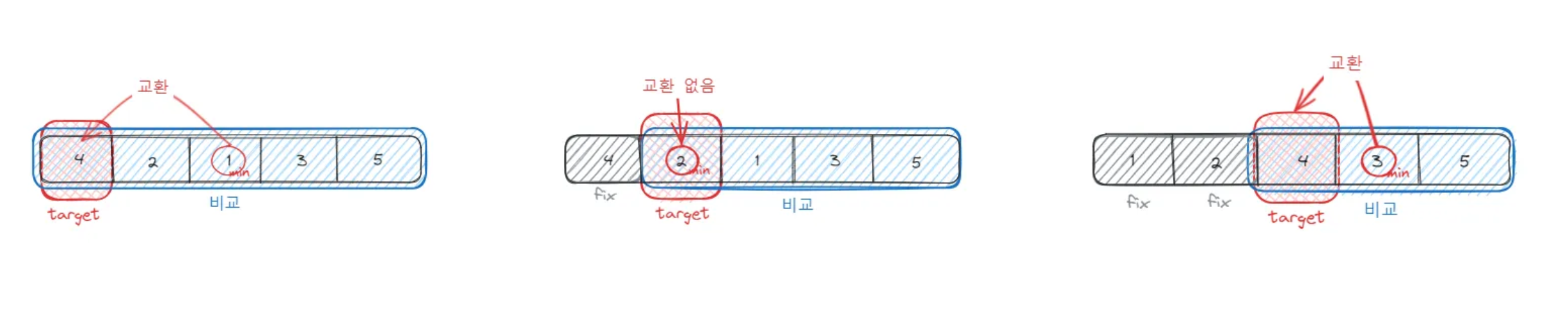
선택 정렬은 배열의 모든 요소를 비교하여 해당되는 위치에 요소를 삽입함으로써 정렬을 완성하는 알고리즘입니다.

1. 첫 요소를 기준삼아 시작합니다.
2. 배열에서 최솟값을 찾아 첫 요소와 교환합니다.
3. 두 번째 요소부터 시작해 최솟값을 찾아 두 번째 요소와 교환합니다.
4. 2의 과정을 매 위치에서 반복합니다.

▪︎ 삽입 정렬

삽입 정렬은 매 순서마다 해당 요소를 삽입할 위치를 찾아 정렬을 완성하는 알고리즘입니다.

1. 정렬되지 않은 첫 요소를 목표로 진행합니다.
2. 두 번째 요소가 첫 번째 요소보다 작다면 자리를 교환합니다.
3. 세 번째 요소와 두 번째 요소를 비교하여 교환하고, 교환했다면 그 이전 요소와 다시 비교 / 두 번째 요소보다 크다면 네 번째 요소로 넘어갑니다.
4. 2의 과정을 매 위치에서 반복합니다.

▪︎ 버블 정렬

버블 정렬은 인접한 두 요소를 비교하여 정렬하는 알고리즘입니다. 가장 큰 요소부터 마지막 인덱스에 위치시키기 때문에 요소의 이동이 마치 거품이 수면으로 올라오는 듯한 모습을 보입니다.

1. 정렬되지 않은 마지막 요소를 목표로 진행합니다.
2. 첫 요소와 다음 요소를 비교 첫 요소가 크다면 두 번째 요소와 자리를 교환합니다.
3. 두 번째 요소와 그 다음 요소를 비교 두 번째 요소가 크다면 세 번째 요소와 자리를 교환합니다.
4. 동작을 반복하면 마지막 요소에 배열의 가장 큰 값이 위치하게 됩니다.
5. 이후 1-3 과정을 반복합니다.

▪︎ 문제 적용

▫︎ 선택 정렬 풀이

function solution(arr) {
  let answer = [...arr];

  for (let i = 0; i < arr.length; i++) {
    for (let j = i; j < arr.length; j++) {
      if (answer[i] <= answer[j]) continue;

      [answer[i], answer[j]] = [answer[j], answer[i]];
    }
  }

  return answer;
}

▫︎ 삽입 정렬 풀이

function solution(arr) {
  const answer = [...arr];

  for (let i = 1; i < answer.length; i++) {
    for (let j = i; j > 0; j--) {
      if (answer[j] < answer[j - 1]) [answer[j], answer[j - 1]] = [answer[j - 1], answer[j]];
      else break;
    }
  }

  return answer;
}

▫︎ 버블 정렬 풀이

function solution(arr) {
  let answer = [...arr];

  for (let i = arr.length - 1; i > 0; i--) {
    for (let j = 0; j < arr.length - i; j++) {
      if (answer[j] <= answer[j + 1]) continue;

      [answer[j], answer[j + 1]] = [answer[j + 1], answer[j]];
    }
  }

  return answer;
}